广东省竞赛分解方程是数学领域中一项重要的竞赛活动,旨在培养学生在数学领域的创新能力和解决问题的能力,分解方程是数学中的一项基础技能,也是解决实际问题的重要工具,本文将介绍广东省竞赛分解方程的背景和意义,阐述分解方程的基本概念和解题方法,并通过具体实例来展示分解方程的实用性和趣味性。
广东省竞赛分解方程的背景和意义
广东省竞赛分解方程是广东省内一项重要的数学竞赛活动,旨在推动数学领域的发展,提高学生的数学素养和解决问题的能力,分解方程作为数学中的一项基础技能,对于培养学生的逻辑思维能力和数学应用能力具有重要意义,通过参加竞赛,学生不仅能够掌握分解方程的解题技巧,还能够培养创新思维和团队协作精神,为未来的学习和工作打下坚实的基础。
分解方程的基本概念和解题方法
分解方程是指将一个复杂的方程分解成若干个简单的方程,以便更容易地求解,分解方程的常用方法包括因式分解法、换元法、配方法等,在解题过程中,需要根据方程的特点选择合适的解题方法,并运用数学知识和技巧进行求解。
具体实例展示分解方程的实用性和趣味性
1、实际问题转化为分解方程
很多实际问题可以通过建立数学模型转化为分解方程的问题,在物理学中,牛顿第二定律可以转化为一个二次方程,通过求解这个二次方程可以得到物体的运动规律,在化学中,化学反应速率的问题也可以通过建立微分方程模型来求解,这些实例表明,分解方程不仅具有实用性,而且具有趣味性。
2、竞赛中的分解方程问题
广东省竞赛中的分解方程问题通常具有一定的难度和挑战性,可能会涉及到一些高次方程、分式方程、参数方程等复杂方程的求解,在解题过程中,需要灵活运用各种解题方法,并结合实际情况进行分析和推理,下面是一个具体的竞赛题目实例:
设实数x满足x^2 + 2ax + 3a = 0与x^2 + 4ax + 3a + 2 = 0至少有一个根大于零小于一,求实数a的取值范围,这个问题需要通过分析一元二次方程的解的性质,结合数形结合的思想进行求解,通过求解这个问题,可以培养学生的分析能力和解决问题的能力,这个问题也展示了分解方程的实用性和趣味性,通过参加竞赛,学生不仅能够掌握分解方程的解题技巧和方法论,还能够培养创新思维和团队协作精神,竞赛中的团队合作环节也是培养学生协作能力和沟通能力的重要途径,在竞赛过程中,学生需要与队友共同讨论问题、分享思路和方法,这种团队协作的精神有助于培养学生的集体荣誉感和责任感,竞赛中的挑战性和压力也能够锻炼学生的意志品质和心理素质,通过参加竞赛,学生可以更好地认识自己、挑战自己、超越自己,成长为具有创新精神和实践能力的优秀人才,结论广东省竞赛分解方程是数学领域中一项重要的竞赛活动,旨在培养学生在数学领域的创新能力和解决问题的能力,通过参加竞赛,学生不仅能够掌握分解方程的解题技巧和方法论,还能够培养创新思维和团队协作精神,分解方程作为数学中的一项基础技能,在解决实际问题中具有广泛的应用和实用性,我们应该重视分解方程的学习和竞赛活动,不断提高学生的数学素养和解决问题的能力。
转载请注明来自天云阁江湖,本文标题:《广东省竞赛分解方程,探索与实践》

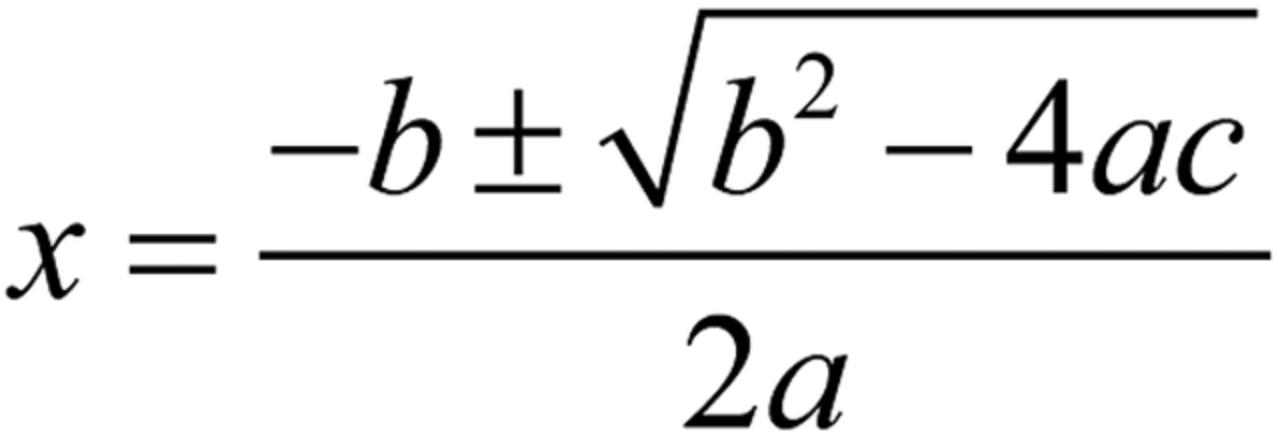







 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号